PriorityBlockingQueue

PriorityBlockingQueue

PriorityBlockingQueue是一个支持优先级的无界阻塞队列，底层采用二叉堆实现的。默认情况下元素采用自然顺序升序排序，当然我们也可以通过构造函数来指定Comparator来对元素进行排序。需要注意的是PriorityBlockingQueue不能保证同优先级元素的顺序。ArrayBlockingQueue、LinkedBlockingQueue都是采用FIFO原则来确定线程执行的先后顺序

二叉堆

定义

父节点的键值总是保持固定的序关系于任何一个子节点的键值，且每个节点的左子树和右子树都是一个二叉堆。它有两种表现形式：最大堆、最小堆。 最大堆：父节点的键值总是大于或等于任何一个子节点的键值， 最小堆：父节点的键值总是小于或等于任何一个子节点的键值。

二叉堆一般用数组表示，如果父节点的节点位置在n处，那么其左孩子节点为：2 * n + 1 ，其右孩子节点为2 * (n + 1)，其父节点为（n - 1） / 2 处。

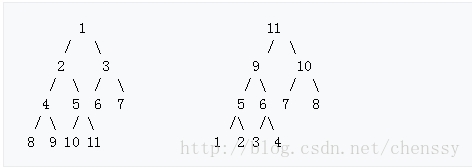
添加元素

最小堆为例：首先将要添加的元素N插添加到堆的末尾位置（在二叉堆中我们称之为空穴）。如果元素N放入空穴中而不破坏堆的序（其值大于跟父节点值（最大堆是小于父节点）），那么插入完成。否则，我们则将该元素N的节点与其父节点进行交换，然后与其新父节点进行比较直到它的父节点不在比它小（最大堆是大）或者到达根节点。

删除元素

删除元素与增加元素一样，需要维护整个二叉堆的序。删除位置1的元素（数组下标0），则把最后一个元素空出来移到最前边，然后和它的两个子节点比较，如果两个子节点中较小的节点小于该节点，就将他们交换，直到两个子节点都比该元素大为止。

定义

内部也是用可重入锁ReentrantLock实现同步机制，但只有一个notEmpty的Condition，ArrayBlockingQueue定义了两个Condition，之所以这样，因为PriorityBlockingQueue是一个无界队列，插入总是会成功，除非消耗尽了资源导致服务器挂。

public class PriorityBlockingQueue<E> extends AbstractQueue<E>
    implements BlockingQueue<E>, java.io.Serializable {
    // 默认容量
    private static final int DEFAULT_INITIAL_CAPACITY = 11;
    // 最大容量
    private static final int MAX_ARRAY_SIZE = Integer.MAX_VALUE - 8;
    // 二叉堆数组
    private transient Object[] queue;
    // 队列元素的个数
    private transient int size;
    // 比较器，如果为空，则为自然顺序
    private transient Comparator<? super E> comparator;
    // 内部锁
    private final ReentrantLock lock;
    private final Condition notEmpty;//非空
    //
    private transient volatile int allocationSpinLock;
    // 优先队列：主要用于序列化，这是为了兼容之前的版本。只有在序列化和反序列化才非空
    private PriorityQueue<E> q;
}

三个基本添加方法

add、put、offer，add和put内部直接调用offer

//add
public boolean add(E e) {
    return offer(e);
}
//put
public void put(E e) {
    offer(e); // never need to block
}
//offer
//正如该方法注释所说，插入一个元素到该优先级队列，该队列是无界的，所以这个方法永远都是插入成功的。
public boolean offer(E e) {
    if (e == null)
        throw new NullPointerException();
    final ReentrantLock lock = this.lock;
    lock.lock();
    int n, cap;
    Object[] array;
    while ((n = size) >= (cap = (array = queue).length))
        tryGrow(array, cap);//进行扩容
    try {
        Comparator<? super E> cmp = comparator;//创建队列对象没传入Comparator实现类默认为null
        if (cmp == null)
            siftUpComparable(n, e, array);//自然排序
        else
            siftUpUsingComparator(n, e, array, cmp);//自定义排序
        size = n + 1;
        notEmpty.signal();
    } finally {
        lock.unlock();
    }
    return true;
}

//扩容  通过自旋
private void tryGrow(Object[] array, int oldCap) {
    lock.unlock(); // 不需要锁主锁
    Object[] newArray = null;
    //CAS
    // allocationSpinLock = 0;代表释放了自旋锁
    // allocationSpinLock = 1;代表释放了自旋锁
    if (allocationSpinLock == 0 &&
        UNSAFE.compareAndSwapInt(this, allocationSpinLockOffset,
                                 0, 1)) {//获取自旋锁，即设置为1
        try {
            int newCap = oldCap + ((oldCap < 64) ?
                                   (oldCap + 2) : // grow faster if small
                                   (oldCap >> 1));
            if (newCap - MAX_ARRAY_SIZE > 0) {    // possible overflow
                int minCap = oldCap + 1;
                if (minCap < 0 || minCap > MAX_ARRAY_SIZE)
                    throw new OutOfMemoryError();
                newCap = MAX_ARRAY_SIZE;
            }
            if (newCap > oldCap && queue == array)
                newArray = new Object[newCapmowei];
        } finally {
            allocationSpinLock = 0;// 代表释放了自旋锁
        }
    }
    if (newArray == null) // back off if another thread is allocating
        Thread.yield();
    lock.lock();
    if (newArray != null && queue == array) {
        queue = newArray;
        System.arraycopy(array, 0, newArray, 0, oldCap);
    }
}
//因为底层是二叉堆，所以需要维持二叉堆顺序，插入的时候和父节点比较
//父节点的位置（k - 1) / 2 即：（k - 1) >>> 1 右移一位相当于除以2的1次方
//按顺序插入，自然排序
//k 二叉堆的末尾即元素数量size
private static <T> void siftUpComparable(int k, T x, Object[] array) {
    Comparable<? super T> key = (Comparable<? super T>) x;
    while (k > 0) {
        int parent = (k - 1) >>> 1;
        Object e = array[parent];
        if (key.compareTo((T) e) >= 0)//二者唯一区别
            break;
        array[k] = e;
        k = parent;
    }
    array[k] = key;
}
//按顺序插入，自定义排序
private static <T> void siftUpUsingComparator(int k, T x, Object[] array,
                                              Comparator<? super T> cmp) {
    while (k > 0) {
        int parent = (k - 1) >>> 1;
        Object e = array[parent];
        if (cmp.compare(x, (T) e) >= 0)//二者唯一区别
            break;
        array[k] = e;
        k = parent;
    }
    array[k] = x;
}

常用出队操作

poll、remove方法来执行出队操作。***出队的永远都是第一个元素：array[0]***。remove底层最后还是调用了poll。

public E poll() {
    final ReentrantLock lock = this.lock;
    lock.lock();
    try {
        return dequeue();
    } finally {
        lock.unlock();
    }
}
//按照二叉堆删除元素规则出队，删除第一个，末位的和其他元素比较
private E dequeue() {
    // 没有元素 返回null
    int n = size - 1;
    if (n < 0)
        return null;
    else {
        Object[] array = queue;
        // 出队元素
        E result = (E) array[0];
        // 最后一个元素（也就是插入到空穴中的元素）
        E x = (E) array[n];
        array[n] = null;
        // 根据比较器释放为null，来执行不同的处理
        Comparator<? super E> cmp = comparator;
        if (cmp == null)
            siftDownComparable(0, x, array, n);
        else
            siftDownUsingComparator(0, x, array, n, cmp);
        size = n;
        return result;
    }
}
//自然排序
private static <T> void siftDownComparable(int k, T x, Object[] array,
                                               int n) {
    if (n > 0) {
        Comparable<? super T> key = (Comparable<? super T>)x;
        int half = n >>> 1;           // loop while a non-leaf
        while (k < half) {
            int child = (k << 1) + 1; // assume left child is least
            Object c = array[child];
            int right = child + 1;
            if (right < n &&
                ((Comparable<? super T>) c).compareTo((T) array[right]) > 0)//左右节点比较
                c = array[child = right];
            if (key.compareTo((T) c) <= 0)//该节点和左右节点最小节点比较
                break;
            array[k] = c;
            k = child;
        }
        array[k] = key;
    }
}
//自定义排序
private static <T> void siftDownUsingComparator(int k, T x, Object[] array,
                                                int n,
                                                Comparator<? super T> cmp) {
    if (n > 0) {
        int half = n >>> 1;
        while (k < half) {
            int child = (k << 1) + 1;
            Object c = array[child];
            int right = child + 1;
            if (right < n && cmp.compare((T) c, (T) array[right]) > 0)
                c = array[child = right];
            if (cmp.compare(x, (T) c) <= 0)
                break;
            array[k] = c;
            k = child;
        }
        array[k] = x;
    }
}